Neural Decomposition
Neural network models for dimensionality reduction, such as Variational AutoEncoders (VAEs), can identify latent low-dimensional structures embedded within high-dimensional data. These low-dimensional representations can provide some insight into patterns within datasets but their interpretation relies on how these map back on the original feature set. However the latter requires interpreting what the decoder network has learnt which makes it challenging.
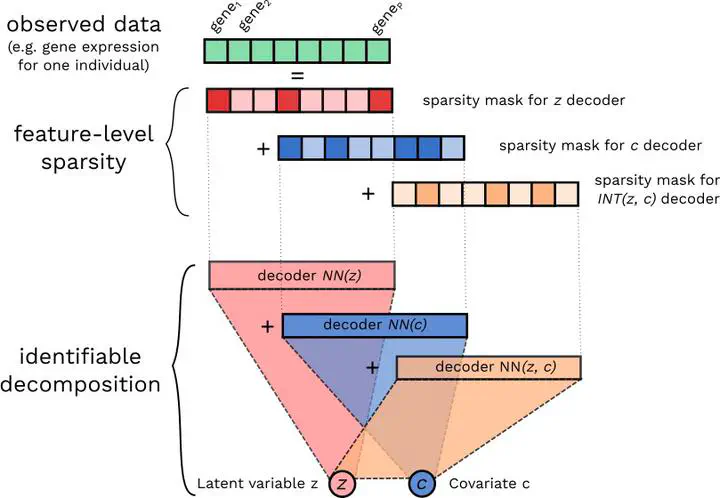
In this project, we have focused on understanding the sources of variation in Conditional VAEs. Our goal is to decompose the feature-level variation in high-dimensional data through disentanglement of additive and interactions effects of latent variables and fixed inputs. We propose to achieve this through the Neural Decomposition - an adaptation of the well-known concept of variance decomposition from classical statistics to deep learning models. We show that identifiable Neural Decomposition relies on training models subject to constraints on the marginal properties of the neural networks whilst naive implementations will lead to non-identifiable models.
Researchers: